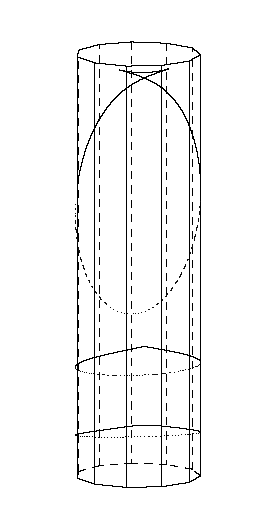
To the right is a cut of null infinity for a Schwarzschild metric where the interior region has a constant density dust solution. We see a cusp ridge of singularities has formed on the cut function.

| My initial research into general relativity centered on the
intersection of null geodesics (light rays) with null infinity.
These intersections, or cuts of null infinity can be used to recreate
the metric of the spacetime in a formulation of GR called the Null
Surface Formulation.
To the right is a cut of null infinity for a Schwarzschild metric where the interior region has a constant density dust solution. We see a cusp ridge of singularities has formed on the cut function. |
 |
 |
Also from “Null cones in
Schwarzschild geometries.” Three different cuts of null infinity with one dimension suppressed. Here we see that the cusp ridge singularity is present only for some cut functions. The singularity first appears as a single point (in the center cut) and then grows into a full blow cusp. |
| Fermat's principle of least time can be used to derive the basic
equations of gravitational lensing theory. In “Fermat
Potentials for Non-Perturbative Gravitational Lensing”, we derived a
generalized version of Fermat's principle, where the envelope of
families of null surfaces led to the derivation of basic lensing
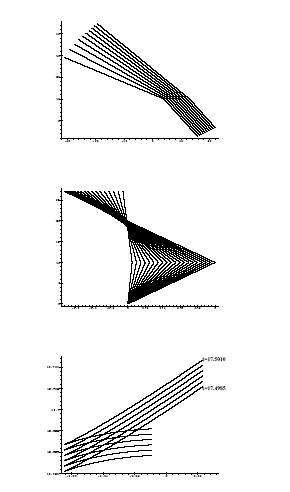
equations. In the top panel, we see the spatial projection of a family of null surfaces that has intersected a lens plane. In the center panel, we see the spatial projection of the envelope showing the light rays. Notice that a caustic line develops. The bottom panel shows the wavefronts associated with the light rays in the center panel. Notice the cusp in the wavefront. |
 |
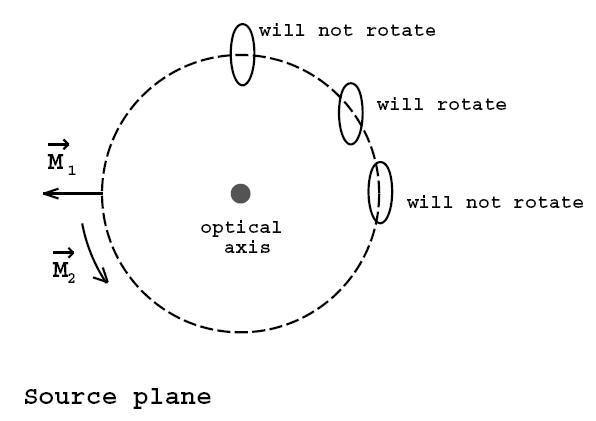 |
We studied the exact disortion of images in a pair of papers “Image
distortion from optical scalars in non-pertubative gravitational lensing”
and “Image
distortion in non-pertubative gravitational lensing.” In the figure to the right, we show how an elliptical source behind a Schwarzschild black hole lens would appear to rotate to an observer. |
| In “Bianchi identity for weak gravitational fields", we show that weak gravitational lensing for thin lenses is governed by the Bianchi identity. Here the measured quantity (the gravitational shear) is directly related the Weyl curvature and the inferred quantity (the mass density) is related to the Ricci curvature. We show for that the Bianchi identity provides the fundamental relation between these two quantities. |
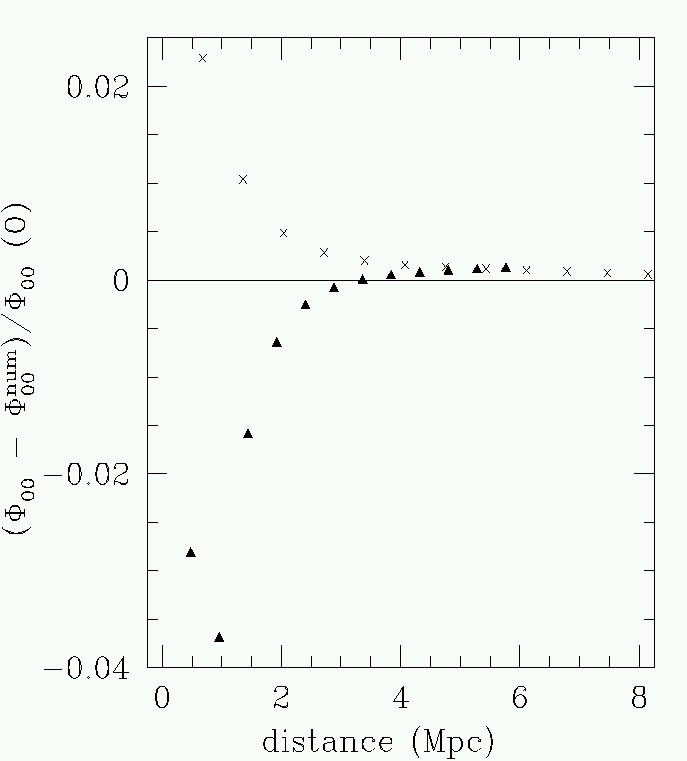
| "Poisson equation for weak gravitational lensing" co-authored by
Bryan Campbell (BSC 2007), carefully examined all the Bianchi identity
components, confirming the results of the previous paper.
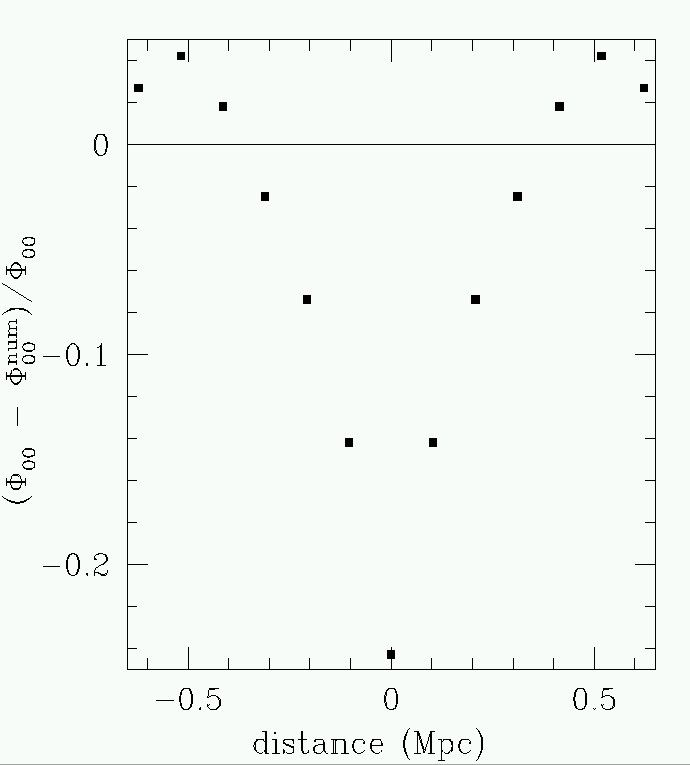
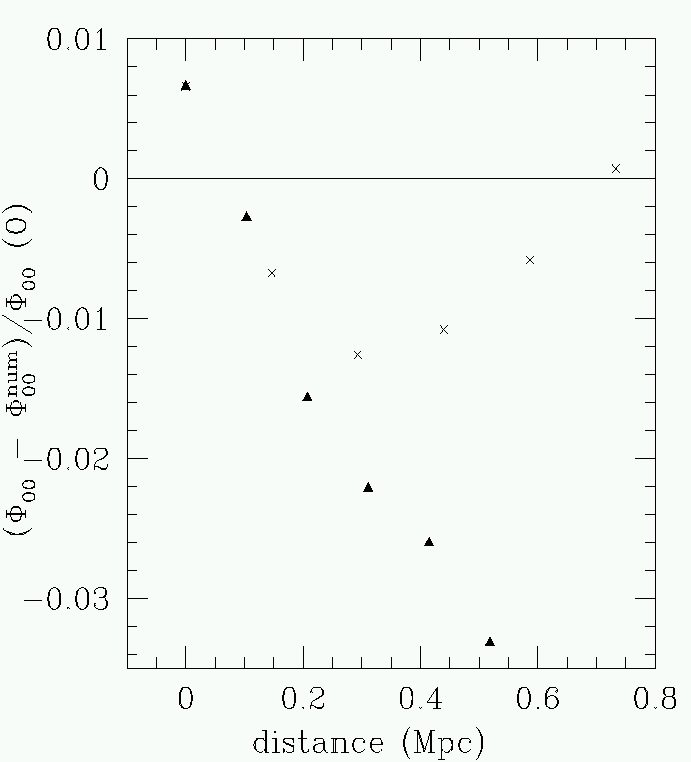
A numerical integration was investigated, and we showed that a significant error in the projected matter density for a ground-based wide-field telescope would be expected, as shown in the figure to the right. If one uses a ground based image to interpolate boundary values to a smaller fov space based image, good results are obtained. Below left, we show the error in the boundary interpolation, while the error in the space-based image for mass density reconstruction in shown below right. |
 |
 |
 |