CHAPTER 9
Capital Budgeting
Techniques
9-3 LG 2, 3: Choosing Between Two Projects with Acceptable Payback Periods
a.
|
Project A |
Project B |
|||||
|
Year |
Cash Inflows |
Investment Balance |
Year |
Cash Inflows |
Investment Balance |
|
|
0 |
-$100,000 |
0 |
-$100,000 |
|||
|
1 |
$10,000 |
-90,000 |
1 |
40,000 |
-60,000 |
|
|
2 |
20,000 |
-70,000 |
2 |
30,000 |
-30,000 |
|
|
3 |
30,000 |
-40,000 |
3 |
20,000 |
-10,000 |
|
|
4 |
40,000 |
0 |
4 |
10,000 |
0 |
|
|
5 |
20,000 |
5 |
20,000 |
|||
Both project A and project B have payback periods of exactly 4 years.
b. Based on the minimum payback acceptance criteria of 4 years set by John Shell both projects should be accepted. However, since they are mutually exclusive projects John should accept project B.
c. Project B is preferred over A because the larger cash flows are in the early years of the project. The quicker cash inflows occur the greater their value.
9-4 LG 3: NPV
PVn = PMT x (PVIFA14%,20 yrs)
a. PVn = $2,000 x 6.623 b. PVn = $3,000 x 6.623
PVn = $13,246 PVn = $19,869
NPV = PVn - Initial investment NPV = PVn - Initial investment
NPV = $13,246 - $10,000 NPV = $19,869 - $25,000
NPV = $3,246 NPV = -$ 5,131
Calculator solution: $3,246.26 Calculator solution: - $5,130.61
Accept Reject
c. PVn = $5,000 x 6.623
PVn = $33,115
NPV = PVn - Initial investment
NPV = $33,115 - $30,000
NPV = $3,115
Calculator solution: $3,115.65
Accept
9-5 LG 3: NPV for Varying Required Returns
PVn = PMT x (PVIFAk%,8 yrs.)
a. 10 % b. 12 %
PVn = $5,000 x (5.335) PVn = $5,000 x (4.968)
PVn = $26,675 PVn = $24,840
NPV = PVn - Initial investment NPV = PVn - Initial investment
NPV = $26,675 - $24,000 NPV = $24,840 - $24,000
NPV = $2,675 NPV = $840
Calculator solution: $2,674.63 Calculator solution: $838.19
Accept; positive NPV Accept; positive NPV
c. 14%
PVn = $5,000 x (4.639)
PVn = $23,195
NPV = PVn - Initial investment
NPV = $23,195 - $24,000
NPV = - $805
Calculator solution: - $805.68
Reject; negative NPV
9-6 LG 2: NPV-Independent Projects
Project A
PVn = PMT x (PVIFA14%,10 yrs.)
PVn = $4,000 x (5.216)
PVn = $20,864
NPV = $20,864 - $26,000
NPV = - $5,136
Calculator solution: - $5,135.54
Reject
Project B-PV of Cash Inflows
Year CF PVIF14%,n PV
1 $100,000 .877 $ 87,700
2 120,000 .769 92,280
3 140,000 .675 94,500
4 160,000 .592 94,720
5 180,000 .519 93,420
6 200,000 .456 91,200
$553,820
NPV = PV of cash inflows - Initial investment = $553,820 - $500,000
NPV = $53,820
Calculator solution: $53,887.93
Accept
Project C-PV of Cash Inflows
Year CF PVIF14%,n PV
1 $20,000 .877 $ 17,540
2 19,000 .769 14,611
3 18,000 .675 12,150
4 17,000 .592 10,064
5 16,000 .519 8,304
6 15,000 .456 6,840
7 14,000 .400 5,600
8 13,000 .351 4,563
9 12,000 .308 3,696
10 11,000 .270 2,970
$86,338
NPV = PV of cash inflows - Initial investment = $86,338 - $170,000
NPV = - $83,662
Calculator solution: - $83,668.24
Reject
Project D
PVn = PMT x (PVIFA14%,8 yrs.)
PVn = $230,000 x 4.639
PVn = $1,066,970
NPV = PVn - Initial investment
NPV = $1,066,970 - $950,000
NPV = $116,970
Calculator solution: $116,938.70
Accept
Project E-PV of Cash Inflows
Year CF PVIF14%,n PV
4 $20,000 .592 $ 11,840
5 30,000 .519 15,570
6 0 0
7 50,000 .400 20,000
8 60,000 .351 21,060
9 70,000 .308 21,560
$90,030
NPV = PV of cash inflows - Initial investment
NPV = $90,030 - $80,000
NPV = $10,030
Calculator solution: $9,963.62
Accept
9-10 LG 2, 3: Payback and NPV
a. Project Payback Period
A $40,000 ¸ $13,000 = 3.08 years
B 3 + ($10,000 ¸ $16,000) = 3.63 years
C 2 + ($5,000 ¸ $13,000) = 2.38 years
Project C, with the shortest payback period, is preferred.
b. Project
A PVn = $13,000 x 3.274
PVn = $42,562
NPV = $42,562 - $40,000
NPV = $2,562
Calculator solution: $2,565.82
B Year CF PVIF16%,n PV
1 $ 7,000 .862 6,034
2 10,000 .743 7,430
3 13,000 .641 8,333
4 16,000 .552 8,832
5 19,000 .476 9,044
$39,673
NPV = $39,673 - $40,000
= - $327
Calculator solution: - $322.53
C Year CF PVIF16%,n PV
1 $19,000 .862 $16,378
2 16,000 .743 11,888
3 13,000 .641 8,333
4 10,000 .552 5,520
5 7,000 .476 3,332
$45,451
NPV = $45,451 - $40,000
NPV = $ 5,451
Calculator solution: $5,454.17
Project C is preferred using the NPV as a decision criterion.
c. At a cost of 16%, Project C has the highest NPV. Because of Project C’s cash flow characteristics, high early-year cash inflows, it has the lowest payback period and the highest NPV.
9-11 LG 4: Internal Rate of Return
IRR is found by solving:
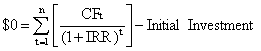
It can be computed to the nearest whole percent by the estimation method as shown for Project A below or by using a financial calculator. (Subsequent IRR problems have been solved with a financial calculator and rounded to the nearest whole percent.)
Project A
Average Annuity = ($20,000 + $25,000 + 30,000 + $35,000 + $40,000) ¸ 5
Average Annuity = $150,000 ¸ 5
Average Annuity = $30,000
PVIFAk%,5yrs. = $90,000 ¸ $30,000 = 3.000
PVIFA19%,5 yrs. = 3.0576
PVlFA20%,5 yrs. = 2.991
However, try 17% and 18% since cash flows are greater in later years.
CFt PVIF17%,t PV@17% PVIF18%,t PV@18%
[(1) x (2)] [(1) x (4)]
Yeart (1) (2) (3) (4) (5)
1 $20,000 .855 $17,100 .847 $16,940
2 25,000 .731 18,275 .718 17,950
3 30,000 .624 18,720 .609 18,270
4 35,000 .534 18,690 .516 18,060
5 40,000 .456 18,240 .437 11,480
$91,025 $88,700
Initial investment - 90,000 - 90,000
NPV $ 1,025 - $ 1,300
NPV at 17% is closer to $0, so IRR 17%, if the firm's cost of capital is below 17%, the project would be acceptable.
Calculator solution: 17.43%
Project B
PVn = PMT x (PVIFAk%,4 yrs.)
$490,000 = $150,000 x (PVIFAk%,4 yrs.)
$490,000 ¸ $150,000 = (PVIFAk%,4 yrs.)
3.27 = PVIFAk%,4
8% < IRR < 9%
Calculator solution: IRR = 8.62%
The firm's maximum cost of capital for project acceptability would be 8% (8.62%).
Project C
PVn = PMT x (PVIFAk%,5 yrs.)
$20,000 = $7,500 x (PVIFAk%,5 yrs.)
$20,000 ¸ $7,500 = (PVIFAk%,5 yrs.)
2.67 = PVIFAk%,5 yrs.
25% < IRR < 26%
Calculator solution: IRR = 25.41%
The firm's maximum cost of capital for project acceptability would be 25% (25.41%).
Project D
![]()
IRR = 21%; Calculator solution: IRR = 21.16%
9-12 LG 4: IRR-Mutually Exclusive Projects
a. and b.
Project X
![]()
IRR = 16%; since IRR > cost of capital, accept.
Calculator solution: 15.67%
Project Y
![]()
IRR = 17%; since IRR > cost of capital, accept.
Calculator solution: 17.29%
c. Project Y, with the higher IRR, is preferred, although both are acceptable.
9-13 LG 2: IRR, Investment Life, and Cash Inflows
a. PVn = PMT x (PVIFAk%,n)
$61,450 = $10,000 x (PVIFA k%,10 yrs.)
$61,450 ¸ $10,000 = PVIFAk%,10 Yrs.
6.145 = PVIFAk%,10 yrs.
k = IRR = 10% (calculator solution: 10.0%)
The IRR < cost of capital; reject the project.
b. PVn = PMT x (PVIFA5%,n)
$61,450 = $10,000 x (PVIFA5%,n)
$61,450 ¸ $10,000 = PVIFA15%,n
6.145 = PVIFA5%,n
18 yrs. < n < 19 yrs.
Calculator solution: 18.23 years
c. PVn = PMT x (PVIFA15%,10)
$61,450 = PMT x (5.019)
$61,450 ¸ 5.019 = PMT
$12,243.48 = PMT
Calculator solution: $12,244.04
9-14 LG 2: NPV and IRR
a. PVn = PMT x (PVIFA10%,7 yrs.)
PVn = $4,000 x (4.868)
PVn = $19,472
NPV = PVn - Initial investment
NPV = $19,472 - $18,250
NPV = $1,222
Calculator solution: $1,223.68
b. PVn = PMT x (PVIFAk%,n)
$18,250 = $4,000 x (PVIFAk%,7yrs.)
$18,250 ¸ $4,000 = (PVIFAk%,7 yrs.)
4.563 = PVIFAk%,7 yrs.
IRR = 12%
Calculator solution: 12.01%
c. The project should be accepted since the NPV > 0 and the IRR > the cost of capital.
9-15 LG 3: NPV, with Rankings
a. NPVA = $20,000(PVIFA15%,3) - $50,000
NPVA = $20,000(2.283) - $50,000
NPVA = $45,660 - $50,000 = - $4,340
Calculator solution: - $4,335.50
Reject
NPVB = $35,000(PVIF15%,1) + $50,000(PVIFA15%,2)(PVIF15%,1) - $100,000
NPVB = $35,000(.870) + $50,000(1.626)(.870) - $100,000
NPVB = $30,450 + $70,731- $100,000 = $1,181
Calculator solution: $1,117.78
Accept
NPVC = $20,000(PVIF15%,1) + $40,000(PVIF15%,2) + $60,000(PVIF15%,3) - $80,000
NPVC = $20,000(.870) + $40,000(.756) + $60,000(.658) - $80,000
NPVC = $17,400 + $30,240 + 39,480 - $80,000 = $7,120
Calculator solution: $7,088.02
Accept
NPVD = $100,000(PVIF15%,1) + $80,000(PVIF15%,2) + $60,000(PVIF15%,3)
- $180,000
NPVD = $100,000(.870) + $80,000(.756) + $60,000(.658) - $180,000
NPVD = $17,400 + $60,480 + 39,480 - $180,000 = $6,640
Calculator solution: $6,898.99
Accept
b. Rank Press NPV
1 C $7,120
2 D 6,640
3 B 1,181
c. Using the calculator the IRRs of the projects are:
Project IRR
A 9.70%
B 15.63%
C 19.44%
D 17.51%
Since the lowest IRR is 9.7% all of the projects would be acceptable if the cost of capital was approximately 10%.
NOTE: Since project A was the only reject project from the 4 projects all that was needed to find the minimum acceptable cost of capital was to find the IRR of A.
9-16 LG 2, 3, 4: All Techniques, Conflicting Rankings
a.
|
Project A |
Project B |
|||||
|
Year |
Cash Inflows |
Investment Balance |
Year |
Cash Inflows |
Investment Balance |
|
|
0 |
-$150,000 |
0 |
-$150,000 |
|||
|
1 |
$45,000 |
-105,000 |
1 |
$75,000 |
-75,000 |
|
|
2 |
45,000 |
-60,000 |
2 |
60,000 |
-15,000 |
|
|
3 |
45,000 |
-15,000 |
3 |
30,000 |
+15,000 |
|
|
4 |
45,000 |
+30,000 |
4 |
30,000 |
0 |
|
|
5 |
45,000 |
30,000 |
||||
|
6 |
45,000 |
30,000 |
||||
![]()
![]()
b. NPVA = $45,000(PVIFA0%,6) - $150,000
NPVA = $45,000(6) - $150,000
NPVA = $270,000 - $150,000 = $120,000
Calculator solution: $120,000
NPVB = $75,000(PVIF0%,1) + $60,000(PVIF0%,2) + $30,000(PVIFA0%,4)(PVIF0%,2)
-$150,000
NPVB = $75,000 + $60,000 + $30,000(4) - $150,000
NPVB = $75,000 + $60,000 + $120,000 - $150,000 = $105,000
Calculator solution: $105,000
c. NPVA = $45,000(PVIFA9%,6) - $150,000
NPVA = $45,000(4.486) - $150,000
NPVA = $201,870 - $150,000 = $51,870
Calculator solution: $51,886.34
NPVB = $75,000(PVIF9%,1) + $60,000(PVIF9%,2) + $30,000(PVIFA9%,4)(PVIF9%,2)
-$150,000
NPVB = $75,000(.917) + $60,000(.842) + $30,000(3.24)(.842) - $150,000
NPVB = $68,775 + $50,520 + $81,842 - $150,000 = $51,137
Calculator solution: $51,112.36
d. Using a financial calculator:
IRRA = 19.91%
IRRB = 22.71%
e.
|
Rank |
|||
|
Project |
Payback |
NPV |
IRR |
|
A |
2 |
1 |
2 |
|
B |
1 |
2 |
1 |
The project that should be selected is A. The conflict between NPV and IRR is due partially to the reinvestment rate assumption. The assumed reinvestment rate of project B is 22.71%, the project's IRR. The reinvestment rate assumption of A is 9%, the firm's cost of capital.
9-17 LG 2, 3: Payback, NPV, and IRR
a. Payback period
3 + ($20,000 ¸ $35,000) = 3.57 years
b. PV of cash inflows
Year CF PVIF12%,n PV
1 $20,000 .893 $ 17,860
2 25,000 .797 19,925
3 30,000 .712 21,360
4 35,000 .636 22,260
5 40,000 .567 22,680
$104,085
NPV = PV of cash inflows - Initial investment
NPV = $104,085 - $95,000
NPV = $9,085
Calculator solution: $9,080.61
c. ![]()
IRR = 15%
Calculator solution: 15.36%
d. NPV = $9,085; since NPV > 0; accept
IRR = 15%; since IRR > 12% cost of capital; accept
The project should be implemented since it meets the decision criteria for both NPV and IRR.
9-18 LG 3, 4, 5: NPV, IRR, and NPV Profiles
a. and b.
Project A
PV of cash inflows:
Year CF PVIF12%,n PV
1 $25,000 .893 $ 22,325
2 35,000 .797 27,895
3 45,000 .712 32,040
4 50,000 .636 31,800
5 55,000 .567 31,185
$145,245
NPV = PV of cash inflows - Initial investment
NPV = $145,245 - $130,000
NPV = $15,245
Calculator solution: $15,237.71
![]()
IRR = 16%
Calculator solution: 16.06%
Project B
PV of cash inflows:
Year CF PVIF15%,n PV
1 $40,000 .893 $ 35,720
2 35,000 .797 27,895
3 30,000 .712 21,360
4 10,000 .636 6,360
5 5,000 .567 2,835
$ 94,170
NPV = $94,170 - $85,000
NPV = $9,170
Calculator solution: $9,161.79
![]()
IRR = 18%
Calculator solution: 17.75%
c.
|
Net Present Value Profile |
|
|
|
Net Present Value ($) |
|
Discount Rate (%) |
Data for NPV Profiles
Discount Rate NPV
A B
0% $ 80,000 $ 35,000
12% $ 15,245 -
15% - $ 9,170
16% 0 -
18% - 0
d. The net present value profile indicates that there are conflicting rankings at a discount rate lower than the intersection point of the two profiles (approximately 15%). The conflict in rankings is caused by the relative cash flow pattern of the two projects. At discount rates above 15%, Project B is preferable; below 15%, Project A is better.
e. Project A has an increasing cash flow from year 1 through year 5, whereas Project B has a decreasing cash flow from year 1 through year 5. Cash flows moving in opposite directions often cause conflicting rankings.
9-19 LG 2, 3, 4, 5, 6: All Techniques-Mutually Exclusive Investment Decision
Project
A B C
Cash inflows (years 1 - 5) $20,000 $31,500 $32,500
a. Payback* 3 years 3.2 years 3.4 years
b. NPV* $10,340 $10,786 $ 4,303
c. IRR* 20% 17% 15%
* Supporting calculations shown below:
a. Payback Period: Project A: $60,000 ¸ $20,000 = 3 years
Project B: $100,000 ¸ $31,500 = 3.2 years
Project C: $110,000 ¸ $32,500 = 3.4 years
b. NPV c. IRR
Project A Project, A
PVn = PMT x (PVIFA13%,5 Yrs.) NPV at 19% = $1,152.70
PVn = $20,000 x 3.517 NPV at 20% = - $ 187.76
PVn = 70,340 Since NPV is closer to zero
at 20%, IRR = 20%
NPV = $70,340 - $60,000 Calculator solution: 19.86%
NPV = $10,340
Calculator solution: $10,344.63
Project B Project B
PVn = $31,500.00 x 3.517 NPV at 17% = $779.40
PVn = $110,785.50 NPV at 18% = -$1,494.11
Since NPV is closer to zero
NPV = $110,785.50 - $100,000 at 17%, IRR = 17%
NPV = $10,785.50 Calculator solution: 17.34%
Calculator solution: $10,792.78
Project C Project C
PVn = $32,500.00 x 3.517 NPV at 14% = $1,575.13
PVn = $114,302.50 NPV at 15% = - $1,054.96
Since NPV is closer to zero at
NPV = $114,302.50 - $110,000 15%, IRR = 15%
NPV = $4,302.50 Calculator solution: 14.59%
Calculator solution: $4,310.02
d.
|
Comparative Net Present Value Profiles |
|
|
|
Net Present Value ($) |
|
Discount Rate (%) |
Data for NPV Profiles
Discount Rate NPV
A B C
0% $ 40,000 $ 57,500 $ 52,500
13% $ 10,340 10,786 4,303
15% - - 0
17% - 0 -
20% 0 - -
The difference in the magnitude of the cash flow for each project causes the NPV to compare favorably or unfavorably, depending on the discount rate.
e. Even though A ranks higher in Payback and IRR, financial theorists would argue that B is superior since it has the highest NPV. Adopting B adds $445.50 more to the value of the firm than does A.
9-20 LG 2, 3, 4, 5, 6: All Techniques with NPV Profile-Mutually Exclusive Projects
a. Project A
Payback period
Year 1 + Year 2 + Year 3 = $60,000
Year 4 = $20,000
Initial investment = $80,000
Payback = 3 years + ($20,000 ¸ 30,000)
Payback = 3.67 years
Project B
Payback period
$50,000 ¸ $15,000 = 3.33 years
b. Project A
PV of cash inflows
Year CF PVIF13%,n PV
1 $15,000 .885 $ 13,275
2 20,000 .783 15,660
3 25,000 .693 17,325
4 30,000 .613 18,390
5 35,000 .543 19,005
$83,655
NPV = PV of cash inflows - Initial investment
NPV = $83,655 - $80,000
NPV = $3,655
Calculator solution: $3,659.68
Project B
NPV = PV of cash inflows - Initial investment
PVn = PMT x (PVIFA13%,n)
PVn = $15,000 x 3.517
PVn = $52,755
NPV = $52,755 - $50,000
= $2,755
Calculator solution: $2,758.47
c. Project A
![]()
IRR = 15%
Calculator solution: 14.61%
Project B
$0 = $15,000 x (PVIFA k%,5) - $50,000
IRR = 15%
Calculator solution: 15.24%
|
Net Present Value Profile |
d.
|
Net Present Value ($) |
|
|
|
Discount Rate (%) |
Data for NPV Profiles
Discount Rate NPV
A B
0% $ 45,000 $ 25,000
13% $ 3,655 $ 2,755
14.6% 0 -
15.2% - 0
Intersection -approximately 15%
If cost of capital is above 15%, conflicting rankings occur.
e. Both projects are acceptable. Both have positive NPVs and equivalent IRR's which are greater than the cost of capital. Although Project B has a slightly higher IRR, the rates are very close. Since Project A has a higher NPV, accept Project A.
9-21 LG 2, 3, 4: Integrative--Complete Investment Decision
a. Initial investment:
Installed cost of new press =
Cost of new press $2,200,000
- After-tax proceeds from sale of old asset
Proceeds from sale of existing press (1,200,000)
+ Taxes on sale of existing press * 480,000
Total after-tax proceeds from sale (720,000)
Initial investment $1,480,000
* Book value = $0
$1,200,000 - $0 = $1,200,000 capital gain
$1,200,000 capital gain x (.40) = $ 480,000 tax liability
b.
Calculation of Operating Cash Flows
Net Profits Net Profits Cash
Year Revenues Expenses Depreciation before Taxes Taxes after Taxes Flow
1 $1,600,000 $800,000 $440,000 $360,000 $144,000 $216,000 $656,000
2 1,600,000 800,000 704,000 96,000 38,400 57,600 761,600
3 1,600,000 800,000 418,000 382,000 152,800 229,200 647,200
4 1,600,000 800,000 264,000 536,000 214,400 321,600 585,600
5 1,600,000 800,000 264,000 536,000 214,400 321,600 585,600
6 0 0 110,000 -110,000 -44,000 -66,000 44,000
c. Payback period = 2 years + ($62,400 ¸ $647,200) = 2.1 years
d. PV of cash inflows:
Year CF PVIF11%,n PV
1 $656,000 .901 $591,056
2 761,600 .812 618,419
3 647,200 .731 473,103
4 585,600 .659 385,910
5 585,600 .593 347,261
6 44,000 .535 23,540
$2,439,289
NPV = PV of cash inflows - Initial investment
NPV = $2,439,289 - $1,480,000
NPV = $959,289
Calculator solution: $959,152
![]()
IRR = 35%
Calculator solution: 35.04%
e. The NPV is a positive $959,289 and the IRR of 35% is well above the cost of capital of 11%. Based on both decision criteria, the project should be accepted.
9-22 LG 2, 3: Integrative-Investment Decision
a. Initial investment:
Installed cost of new asset =
Cost of the new machine $1,200,000
+ Installation costs 150,000
Total cost of new machine $1,350,000
- After-tax proceeds from sale of old asset =
Proceeds from sale of existing machine (185,000)
- Tax on sale of existing machine* (79,600)
Total after-tax proceeds from sale (264,600)
+ Increase in net working capital 25,000
Initial investment $1,110,400
* Book value = $384,000
$384,000 -$185,000 = $199,000 loss
$199,000 x.40 = $79,600 tax benefit
Calculation of Operating Cash Flows
New Machine
Reduction in Net Profits Net Profits Cash
Year Operating Costs Depreciation Before Taxes Taxes After Taxes Flow
1 $350,000 $270,000 $ 80,000 $32,000 $ 48,000 $318,000
2 350,000 432,000 - 82,000 - 32,800 - 49,200 382,800
3 350,000 256,500 93,500 37,400 56,100 312,600
4 350,000 162,000 188,000 75,200 112,800 274,800
5 350,000 162,000 188,000 75,200 112,800 274,800
6 0 67,500 - 67,500 - 27,000 - 40,500 27,000
Existing Machine
Net Profits Net Profits Cash
Year Depreciation Before Taxes Taxes After Taxes Flow
1 $152,000 - $152,000 - $60,800 - $91,200 $60,800
2 96,000 - 96,000 - 38,400 - 57,600 38,400
3 96,000 - 96,000 - 38,400 - 57,600 38,400
4 40,000 - 40,000 - 16,000 - 24,000 16,000
5 0 0 0 0 0
Incremental Operating Cash Flows
Incremental
Year New Machine Existing Machine Cash Flow
1 $318,000 $60,800 $257,200
2 382,800 38,400 344,400
3 312,600 38,400 274,200
4 274,800 16,000 258,800
5 274,800 0 274,800
6 27,000 0 27,000
Terminal cash flow:
After-tax proceeds from sale of new asset =
Proceeds from sale of new asset $200,000
- Tax on sale of new asset * (53,000)
Total proceeds-sale of new asset $147,000
- After-tax proceeds from sale of old asset 0
+ Change in net working capital 25,000
Terminal cash flow $172,000
* Book value of new machine at the end of year 5 is $67,500
$200,000 - $67,500 = $132,500 recaptured depreciation
$132,500 x.40 = $53,000 tax liability
b. Year CF PVIF9%,n PV
1 $257,200 .917 $ 235,852
2 344,400 .842 289,985
3 274,200 .772 211,682
4 258,800 .708 183,230
5 274,800 .650 178,620
Terminal
value 172,000 .650 111,800
$1,211,169
NPV = PV of cash inflows - Initial investment
NPV = $1,211,169 - $1,110,400
NPV = $100,769
Calculator solution: $100,900
c.
![]()
IRR = 12.2%
Calculator solution: 12.24%
d. Since the NPV > 0 and the IRR > cost of capital, the new machine should be purchased.
e. 12.24%. The criterion is that the IRR must equal or exceed the cost of capital; therefore, 12.24% is the lowest acceptable IRR.